HARM: A Hint-Based Assertion Miner
Qualification
After the candidate assertions are generated, HARM filters and ranks these assertions according to user-specified metrics.
How to define these metrics?
We can write these metrics using any valid C boolean, relational, arithmetic, bitwise and string operators. HARM also provides functions to calculate various quantities which can them be used in these expressions.
Some examples:
atct: the number of times where the antecedent and the consequent were both true in the given trace.traceLength: the length of the trace.
An example metric given in the paper is $frequency= \frac{atct}{traceLength}$
Users can define two types of metrics:
- Filtering metrics
- Sorting metrics
Filtering
Filtering metrics consist of
- An Expression
- Threshold
HARM evaluates the expression for each assertion and then drops it if the evaluation is lesser than the threshold. Filtering occurs before ranking.
Ranking
Ranking using a single sorting metric is trivial. Since HARM allows us to define multiple metrics, care needs to be taken in ranking them. There are numerous ways to combine multiple metrics (MCDA). The method used by HARM is as follows
$\displaystyle \prod_{m \in \text{Metrics}} = \text{calibrate}(\frac{m(a)}{m(a_{max})})$
Where:
- $m(a_{max})$ represents the maximum score across all assertions for that metric $m$.
- $m(a)$ is the value of metric $m$ for assertion $a$.
- The calibrate function maps the normalized values to an S-curve
calibrate()
The calibrate function is defined as follows
$calibrate(x) = \frac{1}{(1 + e^{(z - kx)})^2}$
where:
- $z, k$ are constants set by the user
- $x$ is the quantity to be calibrated.
This is said to be a modified version of Richard’s curve (Wikipedia), which itself is a generalization of a logistic function. - Richard’s curve is given by $y(t) = A + \frac{K - A}{(C + Qe^{-Bt})^{\frac{1}{v}}}$ - Setting $A = 0, K = 1, C = 1, v = 0.5, Q = e^z, B = k$ we get $y(t) = \frac{1}{(1 + e^{(z - kt)})^2}$
Rationale
The paper only goes over the desired end result of the ranking system - they wanted to eliminate high score in one metric to compensate for low score in another. There was very little detail as to why they have used the above formula. The following rationale is my interpretation.
-
The primary choice made here is the use of $\prod$ instead of the trivial $\sum$. Weighted Product Model is being used here. There are numerous shortcomings in using Weighted Summation Model.
- The rankings can change based on the normalization used.
- The rankings can changed based on shortlisting.
- The rankings favors overachievers over balanced candidates. Please refer to “Add or multiply? A tutorial on ranking and choosing with multiple criteria” for more details.
-
The authors have decided to use max-scaling as their normalization method. Why they didn’t use other normalization methods such as min-max scaling or z-scores is not mentioned nor the rationale for using max-scaling.
-
While normalization puts all metrics in the same range ([0, 1]), the
calibratefunction introduces a non-linear transformation. This models diminishing returns — a small improvement in a low-scoring metric matters more than a similar improvement in a high-scoring one.
A metaphor from some paper illustrates this:
“A horse, a horse, my kingdom for a horse!”
— Richard III, Act 5, Scene 4, Line 13
When you have zero horses, gaining one is invaluable. But the same isn’t true when you already have 99.
The figure below compares pre- and post-calibration scores:
- Red: Before calibration (linear)
- Blue: After calibration (S-curve)
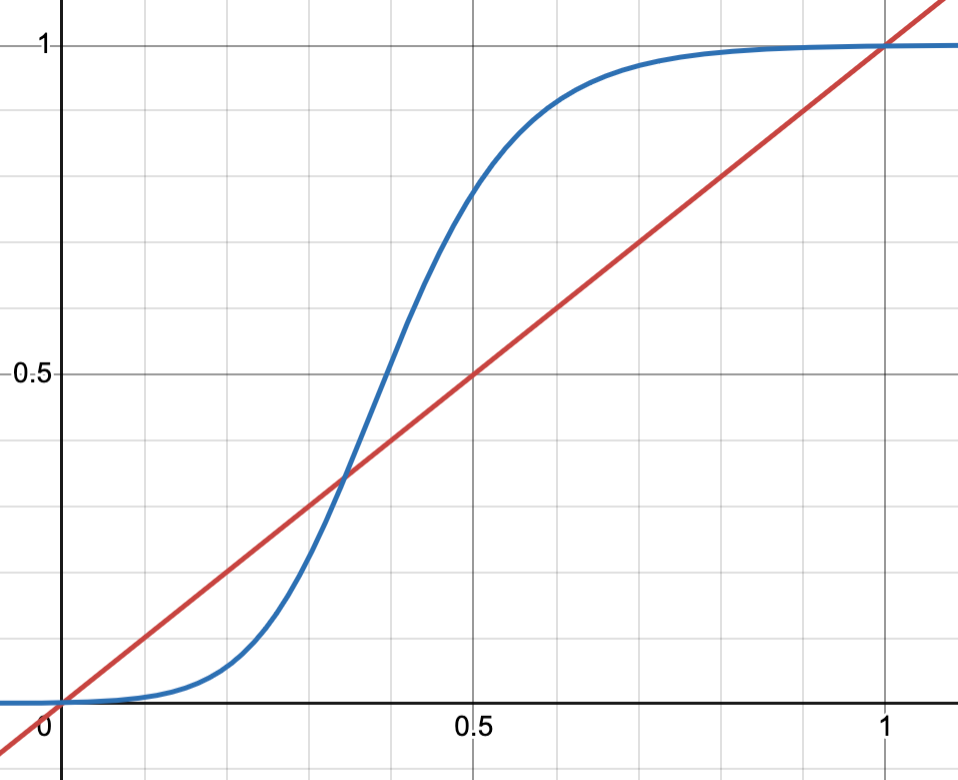
The parameter $z, k$ roughly control where the inflection point occurs.
Summary: HARM’s Ranking Method
- Normalize each metric using max-scaling.
- Apply calibration to introduce non-linearity and model diminishing returns.
- Combine calibrated values using the Weighted Product Model to prevent compensation across metrics.
- The product handles interactions between metrics, while the calibrate function handles non-linear scaling within each metric.